はじめに
Go 言語基礎文法最速マスターにて出題されている演習課題「Exercise: Loops and Functions(ループと関数)」の答えに辿り着くまでの手順と解答例の解説を記事にしてみました。ニュートン法、課題の要件などについても簡単に説明しています。
課題
課題の目的は Sqrt 関数に ニュートン法 を使って平方根の計算を実装することです。
package main
import (
"fmt"
)
func Sqrt(x float64) float64 {
}
func main() {
fmt.Println(Sqrt(2))
}解答例
package main
import (
"fmt"
"math"
)
const cd = 1e-9 // close difference
func Sqrt(x float64) float64 {
z, d := x / 2, 0.
for i := 1; i <= 10; i++ {
z -= (z * z - x) / (2 * z)
if math.Abs(z - d) < cd {
break
}
d = z
}
return z
}
func main() {
fmt.Println(Sqrt(2))
}解説
初めに、ニュートン法について簡単に説明します。
ニュートン法とは、方程式 f(x) = 0 の解を近似的に求めるアルゴリズムです。
適当な値 xn より下記の反復計算式により解の近似値を求めます。
xn + 1 = xn - f(xn) / f'(xn)
反復計算式については、概念図を見ながら考えると理解しやすいです。
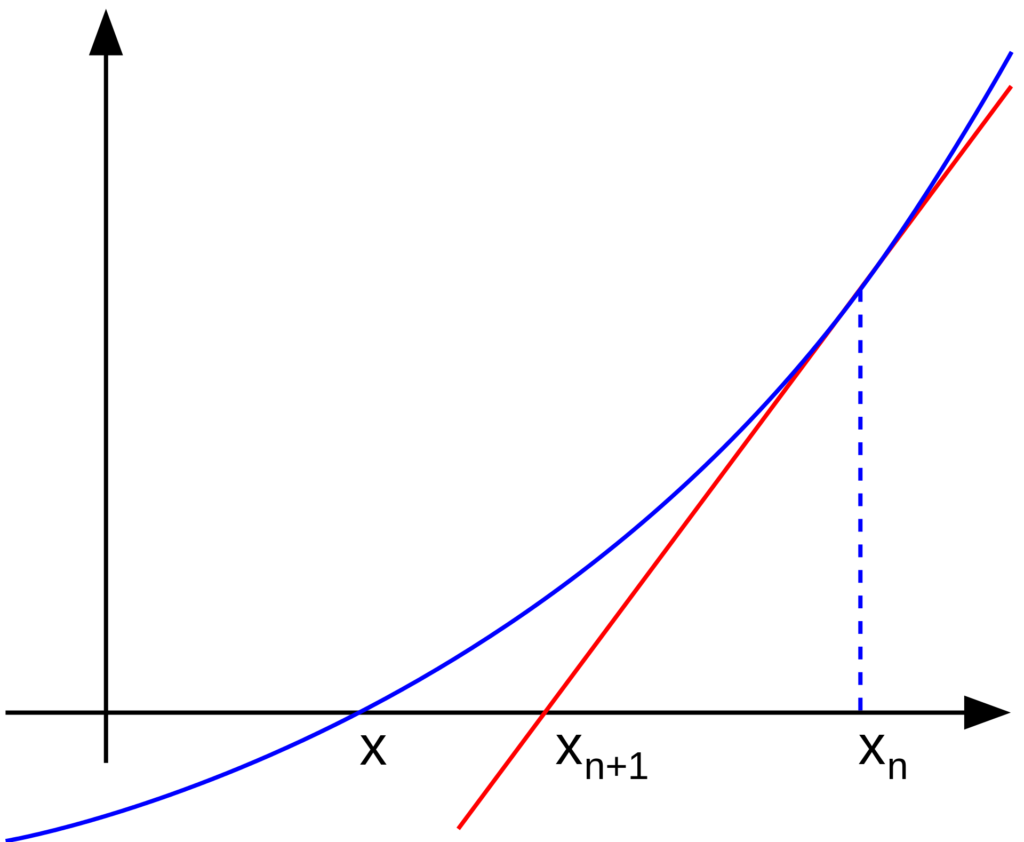
概念図より、ある値 xn を通過する f(x) との接線は (xn,f(xn)) を通過する傾き f'(xn) の直線なので、方程式は y - f(xn) = f'(xn)(x - xn) となります。
この接線は (xn+1,0) を通過するので、方程式の x に xn+1、y に 0 を入れると -f(xn) = f'(xn)(xn + 1 - xn) となります。
この式を xn + 1 = の形にすると反復計算式と同じになりますよね。そして、算出値 xn + 1 を元に同じ計算を繰り返すと x の近似値が求まる、これがニュートン法です。
小難しいことを長々とぬかしおりましたが、ぶっちゃけ下記画像の理解レベルで大丈夫です。

解に収束しない場合や理論の説明はないのかと思う有識者ニキもいると思うんですけど、本題から逸れて数学の解説になってしまうので省略しています。
では、課題のソースコードを読み解いていきます。
7 〜 8 行目、float64 型の引数と戻り値の Sqrt 関数が定義されています。この中に平方根の計算を実装します。
func Sqrt(x float64) float64 {
}10 〜 12 行目、main 関数で Sqrt 関数の戻り値を fmt.Println 関数で出力しています。
func main() {
fmt.Println(Sqrt(2))
}さて、実装を進める前に本課題には下記 5 点の要件が存在します。
- 何が入力されても
zの適切な開始推測値は浮動小数点の1とする。 - 計算を 10 回繰り返して、其々の変数
zを出力する。 - 計算結果の変化量が僅差である場合はループを停止させ、計算回数が 10 回よりも多いか少ないかを確認する。
- 開始推測値に
xやx / 2のような他の値を与えた場合の結果を確認する。 - 関数の結果は標準ライブラリの
math.Sqrtにどれくらい近付いたか比較する。
では、ひとつずつ潰していきましょう。
① を解決するには、変数 z を浮動小数点の 1 で初期化して宣言します。:= という代入文は、暗黙的な型宣言 のことです。
package main
import (
"fmt"
)
func Sqrt(x float64) float64 {
// 開始推測値
z := 1.0
}
func main() {
fmt.Println(Sqrt(2))
}② を解決するには、for 文で平方根の計算を 10 回繰り返し、其々の変数 z を fmt.Println 関数を出力します。平方根の計算式 z -= (zz - x) / (2z) は課題の文章にありましたね。
package main
import (
"fmt"
)
func Sqrt(x float64) float64 {
// 開始推測値
z := 1.0
for i := 1; i <= 10; i++ {
z -= (z * z - x) / (2 * z)
fmt.Println(i, "回目の計算値は", z, "です。")
}
return z
}
func main() {
fmt.Println(Sqrt(2))
}平方根の計算式 z -= (z * z - x) / (2 * z) の z2 - x は z2 が期待値 x からどのぐらい離れているかを表していて、除算の 2z は z2 の変化量に応じて z の調整値を変化させています。
因みに -= という複合代入演算子は、左辺値から右辺値を減算した値を左辺の変数に再代入しています。
実行結果は下記のようになります。
1 回目の計算値は 1.5 です。
2 回目の計算値は 1.4166666666666667 です。
3 回目の計算値は 1.4142156862745099 です。
4 回目の計算値は 1.4142135623746899 です。
5 回目の計算値は 1.4142135623730951 です。
6 回目の計算値は 1.414213562373095 です。
7 回目の計算値は 1.4142135623730951 です。
8 回目の計算値は 1.414213562373095 です。
9 回目の計算値は 1.4142135623730951 です。
10 回目の計算値は 1.414213562373095 です。
1.414213562373095問題なさそうですね。
③ を解決するにはこちらで「僅差」の定義を決める必要がありますね、今回は適当に 1e-9(1 * 10-9, 0.000000001)としましょう。
まずは、1e-9 との絶対差を格納する変数 d(difference)を定義します。数学的に考えるならば Δ(Delta)の d ですね。
func Sqrt(x float64) float64 {
z, d := 1., 0.
for i := 1; i <= 10; i++ {
z -= (z * z - x) / (2 * z)
fmt.Println(i, "回目の計算値は", z, "です。")
}
return z
}次は math パッケージを import して、math.Abs 関数で変数 z と 1e-9 の絶対差を算出します。
その計算を if 文の条件式に記述して「僅差」だった場合は break でループを抜けて変数 z を return します。
「僅差」でない場合は計算を継続します。
package main
import (
"fmt"
"math"
)
func Sqrt(x float64) float64 {
z, d := 1., 0.
for i := 1; i <= 10; i++ {
z -= (z * z - x) / (2 * z)
fmt.Println(i, "回目の計算値は", z, "です。")
if math.Abs(z - d) < 1e-9 {
break
}
d = z
}
return z
}
func main() {
fmt.Println(Sqrt(2))
}実行結果は下記のようになります。
1 回目の計算値は 1.5 です。
2 回目の計算値は 1.4166666666666667 です。
3 回目の計算値は 1.4142156862745099 です。
4 回目の計算値は 1.4142135623746899 です。
5 回目の計算値は 1.4142135623730951 です。
1.41421356237309515 回目の計算で「僅差」だったので 10 回よりも少ないことがわかりました。
④ を解決するには、そのまま開始推測値に x と x / 2 を与えるだけです。
変数 z に仮引数の変数 x を代入してみます。
package main
import (
"fmt"
"math"
)
func Sqrt(x float64) float64 {
z, d := x, 0.
for i := 1; i <= 10; i++ {
z -= (z * z - x) / (2 * z)
fmt.Println(i, "回目の計算値は", z, "です。")
if math.Abs(z - d) < 1e-9 {
break
}
d = z
}
return z
}
func main() {
fmt.Println(Sqrt(2))
}実行結果は下記のようになります、開始推測値が 1 の時と同じですね。
1 回目の計算値は 1.5 です。
2 回目の計算値は 1.4166666666666667 です。
3 回目の計算値は 1.4142156862745099 です。
4 回目の計算値は 1.4142135623746899 です。
5 回目の計算値は 1.4142135623730951 です。
1.4142135623730951変数 z に仮引数の変数 x / 2 を代入してみます。
package main
import (
"fmt"
"math"
)
func Sqrt(x float64) float64 {
z, d := x / 2, 0.
for i := 1; i <= 10; i++ {
z -= (z * z - x) / (2 * z)
fmt.Println(i, "回目の計算値は", z, "です。")
if math.Abs(z - d) < 1e-9 {
break
}
d = z
}
return z
}
func main() {
fmt.Println(Sqrt(2))
}実行結果は下記のようになります、開始推測値が 1., x の時と同じです、興味深いですね。
1 回目の計算値は 1.5 です。
2 回目の計算値は 1.4166666666666667 です。
3 回目の計算値は 1.4142156862745099 です。
4 回目の計算値は 1.4142135623746899 です。
5 回目の計算値は 1.4142135623730951 です。
1.4142135623730951これも問題なさそうですね。
⑤ を解決するには math.Sqrt 関数を main 関数で呼び出し、Sqrt 関数と戻り値を比較します。
package main
import (
"fmt"
"math"
)
func Sqrt(x float64) float64 {
z, d := x / 2, 0.
for i := 1; i <= 10; i++ {
z -= (z * z - x) / (2 * z)
fmt.Println(i, "回目の計算値は", z, "です。")
if math.Abs(z - d) < 1e-9 {
break
}
d = z
}
return z
}
func main() {
x := 2.
fmt.Println(Sqrt(x))
fmt.Println(math.Sqrt(x))
}実行結果は下記のようになります、同じですね。
1 回目の計算値は 1.5 です。
2 回目の計算値は 1.4166666666666667 です。
3 回目の計算値は 1.4142156862745099 です。
4 回目の計算値は 1.4142135623746899 です。
5 回目の計算値は 1.4142135623730951 です。
1.4142135623730951
1.4142135623730951実引数の値を変更して、戻り値を比較してみます。
package main
import (
"fmt"
"math"
)
func Sqrt(x float64) float64 {
z, d := x / 2, 0.
for i := 1; i <= 10; i++ {
z -= (z * z - x) / (2 * z)
if math.Abs(z - d) < 1e-9 {
break
}
d = z
}
return z
}
func main() {
x := 169.
fmt.Println(Sqrt(x) == math.Sqrt(x))
}実行結果は下記のようになります。
trueこれで全ての要件を解決することができました。
え、Sqrt 関数に直接 1e-9 と書くのは マジックナンバー でしょ?馬鹿なの?死ぬの?…だと?
そ れ は そ う !
気になる人は Constants を使いましょう。
package main
import (
"fmt"
"math"
)
const cd = 1e-9 // close difference
func Sqrt(x float64) float64 {
z, d := x / 2, 0.
for i := 1; i <= 10; i++ {
z -= (z * z - x) / (2 * z)
if math.Abs(z - d) < cd {
break
}
d = z
}
return z
}
func main() {
fmt.Println(Sqrt(2))
}ループと関数を学ぶのに最適な課題内容でしたね。
以上です。
おわりに
言葉の定義って大事ですよね、今回で言うと「僅差」のことです。
どんな仕事でも相手と言葉の定義を決めたり確認しないと認識の齟齬が発生しちゃいます。








